13+ Euclid Lemma Formula PNG. A = bq + r where q or r can also be zero. For any two positive integers a and b there exist unique integers q and r.
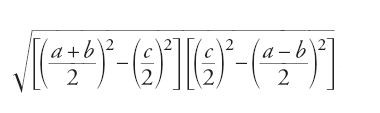
In number theory, euclid's lemma is a lemma that captures a fundamental property of prime numbers, namely:note 1.
So, according to euclid's division lemma, if we have two positive integers a and b, then there would be whole numbers q and r that satisfy the equation: According to euclid's division lemma if we have two positive integers a and b, then there exist unique integers q and r which satisfies the condition a = bq + r. Euclid's lemma, also called euclid's division lemma or euclid's first theorem, is an important lemma. I saw on the internet the following proof of euclid's lemma, which states that if a prime number divides the product of two numbers, then it must remark (added later):


